5.1 Polinomio de interpolación de Newton
Utilizar la matriz de Vandermonde para muchos nodos no es muy buena idea ya
que el tiempo de cálculo para matrices grandes es excesivo. Es mucho más
sencillo utilizar el método clásico de las diferencias divididas de Newton.
Recordemos su definición, para dos nodos, se llama diferencia dividida de orden
uno a :
Mientras que la diferencia dividida de orden n se obtiene por recurrencia a partir
de las anteriores como:
El polinomio de Newton en diferencias divididas es entonces:
p(x)=f[x0]+(x-x0) f[x0,x1]+ (x-x0)(x-x1) f[x0,x1]+ +(x-x0)(x-x1) (x-xn-1)
f[x0,x1, ... , xn]
El polinomio de interpolación con diferencias divididas de Newton, entre otros es la
forma más popular además de las más útil.
Interpolación Lineal
La forma más simple de interpolar es la de conectar dos puntos con una línea
recta. Este método, llamado interpolación lineal, se muestra en la figura:ç
Usando triángulos semejantes, se tiene:
se puede reordenar como :
La cual es una fórmula de interpolación lineal. La notación f 1(X) indica que se
trata de un polinomio de interpolación de primer orden. Nótese que además de
representar la pendiente de la linera que conecta los dos puntos, el termino
Es una aproximación de diferencias divididas finitas a la primera derivada. En
general, entre más pequeño sea el intervalo entre dos puntos, más exacta será la
aproximación.
Interpolación Cuadrática
Una estrategia que mejora la aproximación es la introducir cierta curvatura en la
línea que conecta a los puntos. Si se dispone de tres datos, lo anterior se puede
llevar a cabo con un polinomio de segundo orden (llamado también polinomio
cuadrático o parábola). Una manera conveniente para este caso es :
Nótese que aunque la ecuación [1] parezca diferente de la ecuación general de un
polinomio :
Las dos ecuaciones son equivalentes.
Se puede usar un procedimiento simple para determinar los valores de los
coeficientes. Para bo , se usa la ecuación [4] con X=X0 y se obtiene.
Sustituyendo la ecuación [6] y [4] y evaluando en X=X1 se obtiene:
Y por ultimo las ecuaciones [7] y [6] se sustituyen en la ecuación [4] y se evalúa
está en X=X2 y se obtiene:
Nótese que, al igual que en el caso de interpolación lineal, b1 aun representa la
pendiente de la línea que une los puntos X0 y X1. Por lo tanto, los primeros dos
términos de la ecuación [4] son equivalentes a la interpolación de X0 a X1. El
ultimo termino b2(X-X0) (X-X1), introduce la curvatura de segundo orden de la
formula.
Forma general de los Polinomios de Interpolación de Newton:
Se debe notar que no es necesario que los datos usados en la ecuación [9] estén
igualmente espaciados o que los valores de la abscisa necesariamente se
encuentren en orden ascendente. También nótese que las ecuaciones son
recursivas, esto es las diferencias de orden superior se componen de las
diferencias de orden inferior. Esta propiedad se puede aprovechar al desarrollar un
programa eficiente para un computador.
5.2 Polinomio de interpolación de Lagrange
Se trata de encontrar un polinomio de grado n que pase por los puntos (x0, f(x0)),
(x1, f(x1)), ... (xn, f(xn)), se construye un cociente Ln,k(xk) con la propiedad de que
Ln,k(xi) = 0 cuando i ¹ k y Ln,k(xk) = 1
Se requiere entonces que el numerador contenga
(x – x0) (x – x1)... (x – xk–1)(x – xk+1)... (x – xn)
El denominador debe coincidir con el numerador cuando x = xk.
N-ésimo polinomio interpolante de Lagrange
Teorema
Si x0, x1, x2, ... xn, son n+1 números distintos y si f es una función cuyos valores
están dados en esos números, entonces existe un polinomio de grado a lo más n,
con la propiedad de que
f(xk) = P(xk) para cada k = 0, 1, 2, ...n
Este polinomio está dado por:
Aproximación a 1/x con interpolantesde Lagrange
Usaremos x0 = 2, x1 = 2.5 y x2 = 4, para obtener un polinomio de grado 2 para
1/x. f(x0) = 0.5, f(x1)= 0.4 y f(x2) = 0.25.
Los polinomios de Lagrange son:
P(x) = 0.5*((x–6.5)x+10)+0.4*((–4x+24)x–32)/3+ 0.25*((x + 4.5)x+5)/3
P(x) = (0.05x – 0.425)x + 1.15 = 0.05x2 – 0.425x + 1.15
f(3) = P(3) = 0.325
P(x) = (0.05x – 0.425)x + 1.15
f(3) = P(3) = 0.325
5.3 Interpolación segmentada Esta interpolación se llama interpolación segmentaria o interpolación por splines.
La idea central es que en vez de usar un solo polinomio para interpolar los datos,
podemos usar segmentos de polinomios y unirlos adecuadamente para formar
nuestra interpolación.
Cabe mencionar que entre todas, las splines cúbicas han resultado ser las más
adecuadas para aplicaciones como la mencionada anteriormente.
Así pues, podemos decir de manera informal, que una funcion spline está formada
por varios polinomios, cada uno definido en un intervalo y que se unen entre si
bajo ciertas condiciones de continuidad.
Interpolación Segmentaria Lineal
Este es el caso más sencillo. En él, vamos a interpolar una función f(x) de la que
se nos dan un número N de pares (x,f(x)) por los que tendrá que pasar nuestra
función polinómica P(x). Esta serie de funciones nuestras van a ser lineales, esto
es, con grado 1: de la forma P(x) = ax + b.
Definiremos una de estas funciones por cada par de puntos adyacentes, hasta un
total de (N-1) funciones, haciéndolas pasar obligatoriamente por los puntos que
van a determinarlas, es decir, la función P(x) será el conjunto de segmentos que
unen nodos consecutivos; es por ello que nuestra función será continua en dichos
puntos, pero no derivable en general.
Interpolación Segmentaria Cuadrática
En este caso, los polinomios P(x) a través de los que construimos el Spline tienen
grado 2. Esto quiere decir, que va a tener la forma P(x) = ax² + bx + c
Como en la interpolación segmentaria lineal, vamos a tener N-1 ecuaciones
(donde N son los puntos sobre los que se define la función). La interpolación
cuadrática nos va a asegurar que la función que nosotros generemos a trozos con
los distintos P(x) va a ser continua, ya que para sacar las condiciones que ajusten
el polinomio, vamos a determinar como condiciones:
Que las partes de la función a trozos P(x) pasen por ese punto. Es decir, que las
dos Pn(x) que rodean al f(x) que queremos aproximar, sean igual a f(x) en cada
uno de estos puntos.
Que la derivada en un punto siempre coincida para ambos "lados" de la función
definida a trozos que pasa por tal punto común.
Esto sin embargo no es suficiente, y necesitamos una condición más. ¿Por qué?.
Tenemos 3 incógnitas por cada P(x). En un caso sencillo con f(x) definida en tres
puntos y dos ecuaciones P(x) para aproximarla, vamos a tener seis incógnitas en
total. Para resolver esto necesitaríamos seis ecuaciones, pero vamos a tener tan
sólo cinco: cuatro que igualan el P(x) con el valor de f(x) en ese punto (dos por
cada intervalo), y la quinta al igualar la derivada en el punto común a las dos P(x).
Se necesita una sexta ecuación,¿de dónde se extrae? Esto suele hacerse con el
valor de la derivada en algún punto, al que se fuerza uno de los P(x).
Interpolación Segmentaria Cúbica
En este caso, cada polinomio P(x) a través del que construimos los Splines en
[m,n] tiene grado 3. Esto quiere decir, que va a tener la forma P(x) = ax³ + bx² + cx
+ d
En este caso vamos a tener cuatro variables por cada intervalo (a,b,c,d), y una
nueva condición para cada punto común a dos intervalos, respecto a la derivada
segunda:
Que las partes de la función a trozos P(x) pasen por ese punto. Es decir, que las
dos Pn(x) que rodean al f(x) que queremos aproximar, sean igual a f(x) en cada
uno de estos puntos.
Que la derivada en un punto siempre coincida para ambos "lados" de la función
definida a trozos que pasa por tal punto común.
Que la derivada segunda en un punto siempre coincida para ambos "lados" de la
función definida a trozos que pasa por tal punto común.
Como puede deducirse al compararlo con el caso de splines cuadráticos, ahora no
nos va a faltar una sino dos ecuaciones (condiciones) para el número de
incógnitas que tenemos.
La forma de solucionar esto, determina el carácter de los splines cúbicos. Así,
podemos usar:
Splines cúbicos naturales: La forma más típica. La derivada segunda de P se hace
0 para el primer y último punto sobre el que está definido el conjunto de Splines,
esto son, los puntos m y n en el intervalo [m,n].
Dar los valores de la derivada segunda de m y n de forma "manual", en el conjunto
de splines definidos en el intervalo [m,n].
Hacer iguales los valores de la derivada segunda de m y n en el conjunto de
splines definidos en el intervalo [m,n].
5.4 Regresión y Correlación
La correlación y la regresión nos ayudan a comprender la relación entre las variables y a predecir el estado de los pacientes con
respecto a una variable particular de interés.
La correlación examina la fuerza de la relación entre dos variables, ninguna de las cuales se considera la variable que uno está
tratando de predecir (la variable objetivo).
El análisis de regresión examina la capacidad de uno o más factores, llamados variables independientes, para predecir el estado
de un paciente con respecto a la variable objetivo o dependiente.
Las variables independientes y dependientes pueden ser continuas (tomando una amplia gama de valores) o binarias
(dicotómicas, produciendo resultados de sí o no).
Los modelos de regresión pueden usarse para construir reglas de predicción clínica que ayuden a guiar las decisiones clínicas.
Al considerar la regresión y la correlación, los médicos deben prestar más atención a la magnitud de la correlación o al poder
predictivo de la regresión que a si la relación es estadísticamente significativa.
Los clínicos a veces están interesados en la relación entre diferentes factores o "variables". ¿Qué tan bien la impresión de un
pariente de los síntomas y el bienestar de un paciente predice el propio informe del paciente? ¿Qué tan fuerte es la relación
entre el bienestar físico y la función emocional de un paciente? Al responder estas preguntas, nuestro objetivo es mejorar
nuestra comprensión y considerar las implicaciones para la acción.
Si la relación entre las percepciones de los pacientes y las de los familiares de los pacientes no es fuerte, el clínico debe obtener
ambas perspectivas sobre una situación.
Si la función física y emocional solo están débilmente relacionadas, entonces los médicos deben investigar ambas áreas a fondo.
Los médicos pueden estar aún más interesados en hacer predicciones o inferencias causales que en comprender la relación
entre los fenómenos.
5.5 Mínimos Cuadrados
Mínimos cuadrados es una técnica de análisis numérico enmarcada dentro de la optimización matemática, en la que, dados un conjunto de pares ordenados —variable independiente, variable dependiente— y una familia de funciones, se intenta encontrar la función continua, dentro de dicha familia, que mejor se aproxime a los datos (un "mejor ajuste"), de acuerdo con el criterio de mínimo error cuadrático.
En su forma más simple, intenta minimizar la suma de cuadrados de las diferencias en las ordenadas (llamadas residuos) entre los puntos generados por la función elegida y los correspondientes valores en los datos. Específicamente, se llama mínimos cuadrados promedio (LMS) cuando el número de datos medidos es 1 y se usa el método de descenso por gradiente para minimizar el residuo cuadrado. Se puede demostrar que LMS minimiza el residuo cuadrado esperado, con el mínimo de operaciones (por iteración), pero requiere un gran número de iteraciones para converger.
Desde un punto de vista estadístico, un requisito implícito para que funcione el método de mínimos cuadrados es que los errores de cada medida estén distribuidos de forma aleatoria. El teorema de Gauss-Márkov prueba que los estimadores mínimos cuadráticos carecen de sesgo y que el muestreo de datos no tiene que ajustarse, por ejemplo, a una distribución normal. También es importante que los datos a procesar estén bien escogidos, para que permitan visibilidad en las variables que han de ser resueltas (para dar más peso a un dato en particular, véase mínimos cuadrados ponderados).
La técnica de mínimos cuadrados se usa comúnmente en el ajuste de curvas. Muchos otros problemas de optimización pueden expresarse también en forma de mínimos cuadrados, minimizando la energía o maximizando la entropía.
5.6 Problemas de Aplicación
Problema 1
Si dentro de 10 años Adriana tiene el triple de la edad que tiene ahora, ¿qué edad tendrá entonces?
SOLUCIÓN:
Llamamos x a la edad actual de Adriana. Como Adriana tiene ahora x años, dentro de 10 años su edad será x+10. El triple de la edad que tiene ahora es 3⋅x.
Por tanto, la ecuación que expresa que dentro de 10 años la edad será el triple que la actual es
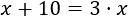
Resolvemos la ecuación:
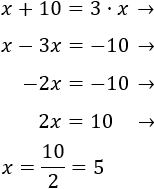
Luego la edad actual de Adriana es 5. Dentro de 10 años, su edad será 15.
Problema 2
Si dentro de 15 años Eduardo tiene el doble de edad que la que tenía hace 5 años, ¿qué edad tiene ahora?
SOLUCIÓN:
Si x es la edad de Eduardo, dentro de 15 años su edad será x+15 y la que tenía hace 5 años era x−5.
Como dentro de 15 años tiene el doble de edad que hace 5 años, tenemos
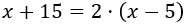
Resolvemos la ecuación:
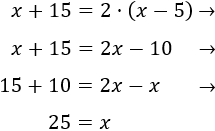
Por tanto, la edad actual de Eduardo es 25.
Problema 3
Calcular el año de nacimiento de Yolanda sabiendo que en 2039 su edad será el doble que en 2018.
SOLUCIÓN:
Si x es la edad que tiene Yolanda en 2018, como en 2039 tendrá el doble, su edad será 2⋅x.
Del 2039 al 2018 hay 21 años de diferencia, así que su edad en 2039 será la edad de 2018 más 21. Es decir, tenemos la ecuación
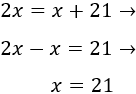
Luego tenemos que la edad de Yolanda en 2018 es 21. Su año de nacimiento es 1997 ya que
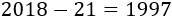
Problema 4
Calcular el año de nacimiento de Ricardo sabiendo que en el año 2003 su edad era el triple que la que tenía en el año 1973.
SOLUCIÓN:
Este problema se resuelve del mismo modo que el anterior.
Si la edad de Ricardo en 1973 era x, su edad en 2003 era 3x. Como 2003-1973 = 30, tenemos
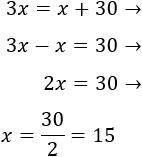
Por tanto, su año de nacimiento es 1958.
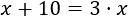
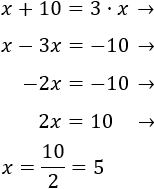
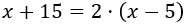
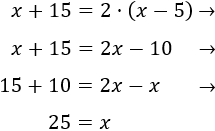
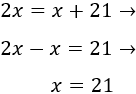
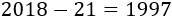
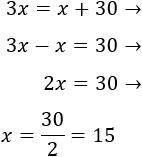














Comentarios
Publicar un comentario