Solución de Ecuaciones Diferenciales

6.1 Métodos de un paso

Los métodos de un paso tienen por objetivo obtener una aproximación de la solución de un problema bien planteado de valor inicial en cada punto de la malla, basándose en el resultado obtenido para el punto anterior.

Se desarrollan aquí los métodos Taylor (incluyendo Euler), y de Runge Kutta. Para ver el detalle de cada uno de los métodos, hacer click en cada uno de los siguientes vínculos. Para volver a esta página, hacer click en la solapa "métodos de un paso".

• Método de Euler

• Métodos de Taylor

• Métodos de Runge Kutta

¿Cómo decidir qué método aplicar?

Hay dos cuestiones importantes que deben tenerse en cuenta al evaluar un algoritmo:

• El esfuerzo computacional requerido para ejecutarlo.

• La precisión que este esfuerzo produce.

Para los algoritmos vistos, el mayor esfuerzo se presenta en la evaluación de f. El algoritmo de Euler hace una evaluación de f por paso y el de RK4 hace cuatro, mientras que los de Taylor, tienen la complicación de evaluar las derivadas de f en cada paso. Por esta razón, y dado que un método de Runge-Kutta de orden m tiene la misma precisión que el método de Taylor de igual orden, es que los métodos de Taylor no se utilizan con fines prácticos.

Por lo dicho anteriormente, el método RK4 requiere cuatro veces más esfuerzo por paso. Este hecho puede resultar engañoso ya que suele obtenerse con pocos pasos de RK4 la misma precisión que con cientos del método de Euler. Por ejemplo, analicemos los resultados obtenidos al aplicar ambos procedimientos en el siguiente PVI:
 

La solución exacta de este problema está dada por y = 2 + 2 t + e^t. El valor aproximado de y(1) obtenido con los métodos de Euler y Runge Kutta y con distintos pasos para cada uno de ellos, arrojó los resultados tabulados en la tabla siguiente:

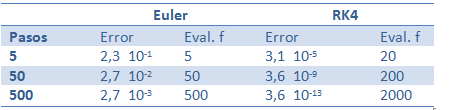
Se observa en esta tabla que al reducir el tamaño del paso en un factor 10, se reduce el error un factor 10 para el método de Euler, y un factor 10000 para el método de Runge-Kutta de orden 4. Esto es consecuencia del error global de cada método. 

 

Consistencia, estabilidad y convergencia

 

Hay algunas propiedades importantes de las ecuaciones en diferencias para problemas de valor inicial de EDOs de primer orden que deben considerarse antes de que se pongan en práctica los métodos numéricos. Ellas son consistencia, estabilidad y convergencia.

 

Se dice que una ecuación en diferencias es consistente con una EDO si la diferencia entre ambas (el error de truncamiento) se acerca a cero a medida que el paso h tiende a cero. En símbolos, si llamamos t_i(h) al error local de truncamiento, podemos decir:

 

Con este concepto se analiza la relación entre la ecuación diferencial y su formulación discreta. Cuando se conoce el error de truncamiento, es fácil probar la consistencia. Cuando no se conoce, debe analizarse la ecuación en diferencias completa para probar la consistencia, utilizando el desarrollo de Taylor.

 

Un método es estable si produce soluciones acotadas cuando la solución exacta es acotada y es inestable cuando produce una solución no acotada cuando la solución exacta es acotada.

 

Hay varias definiciones de estabilidad. Informalmente, se dice que un método es inestable si los errores en las aproximaciones crecen en forma exponencial a medida que el cálculo avanza.

 

Por último, se dice que un método de la ecuación en diferencias de un paso es convergente respecto a la ecuación diferencial que aproxima, si

 

 

Con la convergencia se analiza la relación entre la solución numérica y la solución exacta de la ecuación diferencial. Si se cumplen las condiciones de estabilidad y consistencia en un problema bien planteado, entonces podremos asegurar la convergencia.

 

El método de Runge–Kutta de orden 4 no presenta inestabilidad numérica para valores de h suficientemente pequeños. Pero para el método de Euler estudiado no se puede decir lo mismo.

Por ejemplo, utilicemos este método para resolver el problema:

La solución exacta de esta ecuación está dada por y(t) = e^-t, siendo una función acotada.

 

La ecuación del método de Euler resulta

 

 y_n+1 = y_n + h (- y_n) = (1 – h) y_n = G y_n

 

Aplicando reiteradamente esta fórmula podemos expresar entonces la solución aproximada en función de y₀:

 y_n+1 = (1 – h)ⁿ⁺¹ y₀ , n = 1, …, N.

Se ve en esta ecuación que la solución discreta va a ser acotada siempre que la constante 1-h sea menor a uno en valor absoluto. Esto implica que h debe ser menor a 2, aunque el comportamiento óptimo se da para valores de h entre 0 y 1. Por lo tanto, la solución obtenida con el método de Euler será estable siempre que h sea menor que 2. El hecho de que la estabilidad del método dependa del valor de h, hace que el método sea condicionalmente estable.

Este análisis de estabilidad puede hacerse sólo para ecuaciones diferenciales lineales. En el caso de ecuaciones diferenciales no lineales, deben primero linealizarse localmente, y realizar un análisis de estabilidad en la ecuación de diferencias que aproxima a la ecuación diferencial linealizada.

6.3 Metodo de Pasos Multiples

Los métodos de un paso descritos en las secciones anteriores utilizan información en un solo punto xi para predecir un valor de la variable dependiente yi+1 en un punto futuro xi+1. Procedimientos alternativos, llamados métodos multipaso, se basan en el conocimiento de que una vez empezado el cálculo, se tiene información valiosa de los puntos anteriores y esta a nuestra disposición. La curvatura de las líneas que conectan esos valores previos proporciona información con respecto a la trayectoria de la solución. Los métodos multipaso que exploraremos aprovechan esta información para resolver las EDO. Antes de describir las versiones de orden superior, presentaremos un método simple de segundo orden que sirve para demostrar las características generales de los procedimientos multipaso.

Observe la ecuación ec. 2  alcanza ) a expensas de emplear un tamaño de paso mas grande, 2h. Además, observe que la ecuación ec. 1 no es de autoinicio, ya que involucra un valor previo de la variable dependiente yi-1. Tal valor podria no estar disponible en un problema común de valor inicial. A causa de ello, las ecuaciones 26.11 y 26.12 son llamadas método de Heun de no autoinició.

Como se ilustra en la figura 26.4, la derivada estimada de la ecuación 26.12 se localiza ahora en el punto medio mas que al inicio del intervalo sobre el cual se hace la predicción. Como se demostrara después, esta ubicación centrada mejora el error del predictor a  Sin embargo, antes de proceder a una deducción formal del método de Heun de no autoinicio, resumiremos el método y lo expresaremos usando una nomenclatura ligeramente modificada:

6.3 Ecuaciones Diferenciales Ordinarias

Una ecuación diferencial es una ecuación en que la incógnita es una función: no el valor de la función en uno o varios puntos, sino la función en si misma. Además, la ecuación involucra no solo la función (incógnita), sino también sus derivadas hasta un cierto orden. Cuando la incógnita es una función de una sola variable se dice que la ecuación es ordinaria, debido a que la o las derivadas que aparecen son derivadas ordinarias (por contraposición a las derivadas parciales de las funciones de varias variables). Por ejemplo, y 0 (t) = −y(t) (9.1) es una ecuación diferencial ordinaria (Edo) de primer orden, ya que la máxima derivada que aparece en ella es la de primer orden. Si no resulta confuso se suele escribir también esta ecuación en la forma y 0 = −y, omitiendo la mención expresa a la dependencia de y respecto de t. Resolver esta ecuación consiste en encontrar una o varias funciones y = y(t) que verifiquen la igualdad y 0 (t) = y(t), para todo t perteneciente a un cierto intervalo I. Una tal función se dice que es una solución de la edo. en el intervalo I. Con carácter general, una ecuación diferencial ordinaria de primer orden se escribe: y 0 = f(t, y) (9.2) y se dice que y = y(t) es solución en I de esta ecuación si se verifica y 0 (t) µ = di da(t) ¶ = f(t, y(t)), ∀t ∈ I. (9.3) Por ejemplo, la función y = e −t es solución de la ecuación (9.1) en cualquier intervalo I ⊂ R, ya que y 0 (t) = −e −t = −y(t), ∀t ∈ R. 67 Ecuaciones diferenciales ordinarias 68 Pero también es solución cualquier función de la forma y = Ce−t siendo C una constante arbitraria, puesto que y 0 (t) = −Ce−t = −y(t), ∀t ∈ R. 0 0.5 1 1.5 2 2.5 3 −6 −4 −2 0 2 4 6 Figura 9.1: Curvas de la familia y(t) = Ce−t , soluciones de la ecuación (9.1), para diversos valores de C. Así pues, la ecuación (9.1) tiene infinitas soluciones, lo que no es una particularidad de esta ecuación concreta. La ecuación diferencial ordinaria (9.2) posee, en general, una familia de infinitas soluciones dependientes de una constante arbitraria, a la que se suele llamar solución general de (9.2). Para cada valor de dicha constante arbitraria se obtiene una solución particular. Con frecuencia, en las aplicaciones, lo que interesa es encontrar una solución particular que verifica alguna condición. Por ejemplo, que toma un valor dado para un valor, también dado, de la variable independiente. En este caso, el problema que se plantea se escribe: ½ y 0 = f(t, y) y(t0) = y0 , (9.4) y recibe el nombre de problema de valor valor inicial. El nombre proviene del hecho de que, con frecuencia, la variable independiente, t, representa el tiempo, y el valor t0 es el instante en que comienza un experimento, observación o simulación. En general, si se verifican ciertas condiciones razonables de regularidad de la función f, el problema de valor inicial (9.4) tiene solución ´única. Por ejemplo, el siguiente problema de valor inicial, asociado a la ecuación (9.1), ½ y 0 = −y y(0) = 1 , (9.5) tiene una ´única solución, y = e −t , que se puede encontrar imponiendo la condición inicial, y(0) = 1, a las funciones de la familia de soluciones, y = Ce−t , para deducir para que valor de la constante arbitraria C se cumple la condición. Es decir: y(0) = Ce0 = C = 1 ⇔ C = 1.

6.4 Aplicaciones

Esto es un ejemplo de la aplicación en Ing. mecánica. Consiste de un resorte o muelle en espiral suspendido de un soporte rígido con una masa sujeta al extremo. Para analizar este fenómeno usamos la ley de hooke y la segunda ley de newton. La ley de hooke establece que el resorte ejerce una fuerza de restitución  opuesta a la dirección de alargamiento  del resorte peso=kl donde k es la constante de restitución y l es el alargamiento hasta la posición de equilibrio. Para aplicar la ley de newton, hay q tener en cuenta q sobre la mas m actúa la fuerza de gravedad  (m.g), la fuerza de restitución (-kx-mg donde x es el alargamiento) , la fuerza de amortiguación que es proporcional a la velocidad de la masa )-b(dx/dt) con b la constante de amortiguación ) y las fuerzas externas (F(t)). Así q la ecuación diferencial q resulta es:
 
M  d^2x/dt^2+b dx/dt+kx=f(t)